Plane Areas
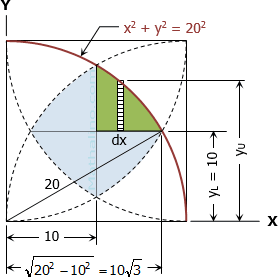
Example 7 | Area inside the square not common to the quarter circles
Problem
The figure shown below is composed of arc of circles with centers at each corner of the square 20 cm by 20 cm. Find the area inside the square but outside the region commonly bounded by the quarter circles. The required area is shaded as shown in the figure below.

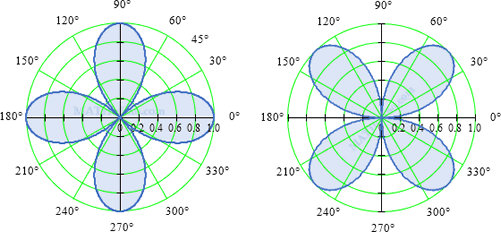
06 Area Within the Curve r^2 = 16 cos θ
Example 6
What is the area within the curve r2 = 16 cos θ?
- Read more about 06 Area Within the Curve r^2 = 16 cos θ
- Log in or register to post comments
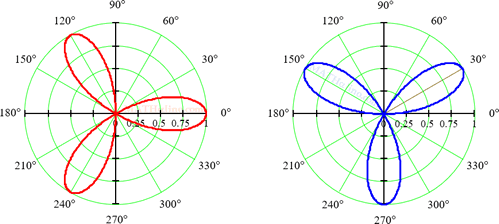
05 Area Enclosed by Four-Leaved Rose r = a cos 2θ
Find the area enclosed by four-leaved rose r = a cos 2θ.
- Read more about 05 Area Enclosed by Four-Leaved Rose r = a cos 2θ
- Log in or register to post comments
Example 6 | Plane Areas in Rectangular Coordinates
Example 6
Find each of the two areas bounded by the curves y = x3 - 4x and y = x2 + 2x.
- Read more about Example 6 | Plane Areas in Rectangular Coordinates
- Log in or register to post comments
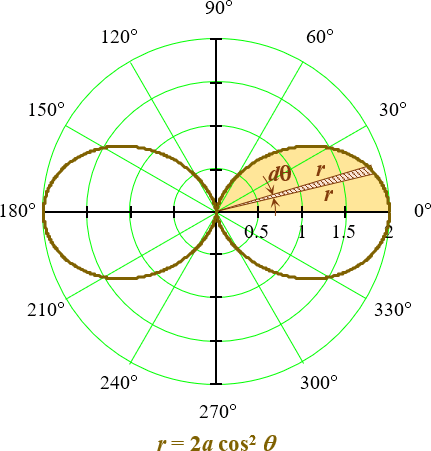
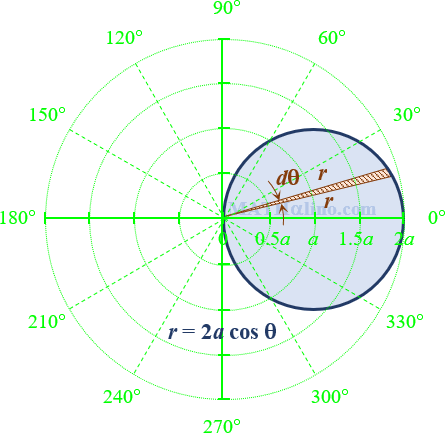
02 Area Bounded by the Lemniscate of Bernoulli r^2 = a^2 cos 2θ
Example 2
Find the area bounded by the lemniscate of Bernoulli r2 = a2 cos 2θ.