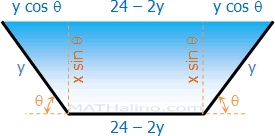Partial Derivatives

Let F be a function of several variables, say x, y, and z. In symbols,

$F = f(x, \, y, \, z)$.

The partial derivative of F with respect to x is denoted by

$\dfrac{\partial F}{\partial x}$

and can be found by differentiating f(x, y, z) in terms of x and treating the variables y and z as constants.
 

Problem 04 | Determination of Integrating Factor

Problem 04
$y(4x + y)~dx - 2(x^2 - y)~dy = 0$
 

Solution 04
$M~dx + N~dy = 0$

$y(4x + y)~dx - 2(x^2 - y)~dy = 0$
 

$M = y(4x + y) = 4xy + y^2$

$N = -2(x^2 - y) = -2x^2 + 2y$
 

$\dfrac{\partial M}{\partial y} = 4x + 2y$

$\dfrac{\partial N}{\partial x} = -4x$
 

$\dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} = (4x + 2y) - (-4x)$

$\dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} = 8x + 2y$
 

Problem 03 | Determination of Integrating Factor

Problem 03
$y(2x - y + 1)~dx + x(3x - 4y + 3)~dy = 0$
 

Solution 03
$M~dx + N~dy = 0$

$y(2x - y + 1)~dx + x(3x - 4y + 3)~dy = 0$
 

$M = y(2x - y + 1) = 2xy - y^2 + y$

$N = x(3x - 4y + 3) = 3x^2 - 4xy + 3x$
 

$\dfrac{\partial M}{\partial y} = 2x - 2y + 1$

$\dfrac{\partial N}{\partial x} = 6x - 4y + 3$
 

$\dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} = (2x - 2y + 1) - (6x - 4y + 3)$

$\dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} = -4x + 2y - 2$

Problem 02 | Determination of Integrating Factor

Problem 02
$2y(x^2 - y + x)~dx + (x^2 - 2y)~dy = 0$
 

Solution 02
$M~dx + N~dy = 0$

$2y(x^2 - y + x)~dx + (x^2 - 2y)~dy = 0$
 

$M = 2y(x^2 - y + x) = 2x^2y - 2y^2 + 2xy$

$N = x^2 - 2y$
 

$\dfrac{\partial M}{\partial y} = 2x^2 - 4y + 2x$

$\dfrac{\partial N}{\partial x} = 2x$
 

$\dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} = (2x^2 - 4y + 2x) - 2x$

$\dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} = 2x^2 - 4y = 2(x^2 - 2y)$
 

Problem 01 | Determination of Integrating Factor

Problem 01
$(x^2 + y^2 + 1)~dx + x(x - 2y)~dy = 0$
 

Solution 01
$M~dx + N~dy = 0$

$(x^2 + y^2 + 1)~dx + x(x - 2y)~dy = 0$
 

$M = x^2 + y^2 + 1$

$N = x(x - 2y) = x^2 - 2xy$
 

$\dfrac{\partial M}{\partial y} = 2y$

$\dfrac{\partial N}{\partial x} = 2x - 2y$
 

$\dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} = 2y - (2x - 2y)$

$\dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} = -2x + 4y$

The Determination of Integrating Factor

From the differential equation
 

$M ~ dx + N ~ dy = 0$

 

Rule 1
If   $\dfrac{1}{N}\left( \dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} \right) = f(x)$,   a function of x alone, then   $u = e^{\int f(x)~dx}$   is the integrating factor.

 

Rule 2
If   $\dfrac{1}{M}\left( \dfrac{\partial M}{\partial y} - \dfrac{\partial N}{\partial x} \right) = f(y)$,   a function of y alone, then   $u = e^{-\int f(y)~dy}$   is the integrating factor.

 

Problem 04 | Exact Equations

Problem 04
$(y^2 - 2xy + 6x) \, dx - (x^2 - 2xy + 2) \, dy = 0$
 

Solution 04
$(y^2 - 2xy + 6x) \, dx - (x^2 - 2xy + 2) \, dy = 0$

$M = y^2 - 2xy + 6x$

$N = -x^2 + 2xy - 2$
 

Test for exactness
$\dfrac{\partial M}{\partial y} = 2y - 2x$

$\dfrac{\partial N}{\partial x} = -2x + 2y$

Exact!
 

Let
$\dfrac{\partial F}{\partial x} = M$

$\dfrac{\partial F}{\partial x} = y^2 - 2xy + 6x$

$\partial F = (y^2 - 2xy + 6x) \, \partial x$
 

Integrate partially in x, holding y as constant

Problem 03 | Exact Equations

Problem 03
$(2xy - 3x^2) \, dx + (x^2 + y) \, dy = 0$
 

Solution 03
$(2xy - 3x^2) \, dx + (x^2 + y) \, dy = 0$
 

$M = 2xy - 3x^2$

$N = x^2 + y$
 

Test for exactness
$\dfrac{\partial M}{\partial y} = 2x$

$\dfrac{\partial N}{\partial x} = 2x$

Exact!
 

Let
$\dfrac{\partial F}{\partial x} = M$

$\dfrac{\partial F}{\partial x} = 2xy - 3x^2$

$\partial F = (2xy - 3x^2) \, \partial x$
 

Integrate partially in x, holding y as constant