Confirmed CE board problems but the date of exam is still unknown or not yet confirmed.

Hollow Circular Beam with Known Cracking Moment

Situation
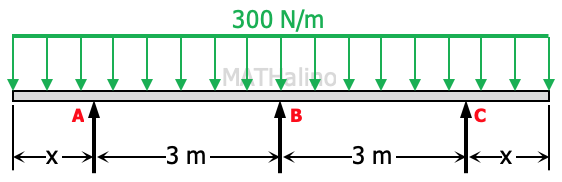
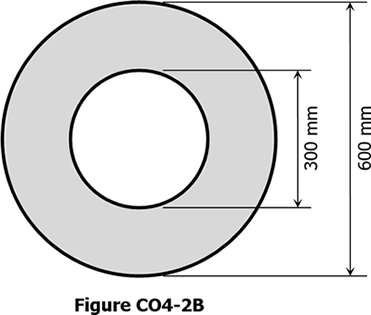
A concrete beam with cross section in Figure CO4-2B is simply supported over a span of 4 m. The cracking moment of the beam is 75 kN·m.
 

figure-co4-2b.jpg

 

1.   Find the maximum uniform load that the beam can carry without causing the concrete to crack, in kN/m.

A.   35.2 C.   33.3
B.   37.5 D.   41.8

2.   Find the modulus of rapture of the concrete used in the beam.

A.   4.12 MPa C.   3.77 MPa
B.   3.25 MPa D.   3.54 MPa

3.   If the hallow portion is replaced with a square section of side 300 mm, what is the cracking moment of the new section in kN·m?

A.   71.51 C.   78.69
B.   76.58 D.   81.11

 

Continuous Beam With Equal Support Reactions

Situation
A beam 100 mm × 150 mm carrying a uniformly distributed load of 300 N/m rests on three supports spaced 3 m apart as shown below. The length x is so calculated in order that the reactions at all supports shall be the same.
 

design-practice-2-given.png

 

1.   Find x in meters.

A.   1.319 C.   1.217
B.   1.139 D.   1.127

2.   Find the moment at B in N·m.

A.   -240 C.   -242
B.   -207 D.   -226

3.   Calculate the reactions in Newton.

A.   843.4 C.   863.8
B.   425.4 D.   827.8

 

Continuous Beam With a Gap and a Zero Moment in Interior Support

Situation
A beam of uniform cross section whose flexural rigidity EI = 2.8 × 1011 N·mm2, is placed on three supports as shown. Support B is at small gap Δ so that the moment at B is zero.
 

design-practice-1-given.gif

 

1.   Calculate the reaction at A.

A.   4.375 kN C.   5.437 kN
B.   8.750 kN D.   6.626 kN

2.   What is the reaction at B?

A.   4.375 kN C.   5.437 kN
B.   8.750 kN D.   6.626 kN

3.   Find the value of Δ.

A.   46 mm C.   34 mm
B.   64 mm D.   56 mm