October 2013

Elementary Applications

Velocity of escape from the earth
Newton's law of cooling
Simple chemical conversion
Logistic growth and price of commodities
Orthogonal trajectories

Newton's Law of Cooling

Newton's Law of Cooling states that the temperature of a body changes at a rate proportional to the difference in temperature between its own temperature and the temperature of its surroundings.

We can therefore write

$\dfrac{dT}{dt} = -k(T - T_s)$

where,
T = temperature of the body at any time, t
T_s = temperature of the surroundings (also called ambient temperature)
T_o = initial temperature of the body
k = constant of proportionality

01 - Thermometer reading after 6 minutes of being outside

Problem 01
A thermometer which has been at the reading of 70°F inside a house is placed outside where the air temperature is 10°F. Three minutes later it is found that the thermometer reading is 25°F. Find the thermometer reading after 6 minutes.

Simple Chemical Conversion

From the results of chemical experimentation of substance converted into another substance, it was found that the rate of change of unconverted substance is proportional to the amount of unconverted substance.

If x is the amount of unconverted substance, then

$\dfrac{dx}{dt} = -kx$

with a condition that x = x_o when t = 0.

$\dfrac{dx}{dt} = -kx$

$\dfrac{dx}{x} = -k \, dt$

$\ln x = -kt + \ln C$

$\ln x = \ln e^{-kt} + \ln C$

$\ln x = \ln Ce^{-kt}$

Read more about Simple Chemical Conversion
Add new comment
31890 reads

01 - Find how long would it take for half amount af radium to decompose

Problem 01
Radium decomposes at a rate proportional to the quantity of radium present. Suppose it is found that in 25 years approximately 1.1% of certain quantity of radium has decomposed. Determine how long (in years) it will take for one-half of the original amount of radium to decompose.

02 - Time to dissipate 90% of certain radioactive substance

Problem 02
A certain radioactive substance has a half-life of 38 hour. Find how long it takes for 90% of the radioactivity to be dissipated.

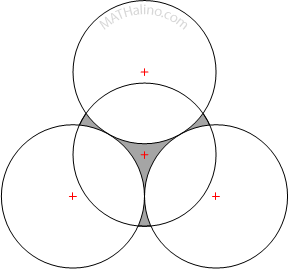
11 - Area inside a circle but outside three other externally tangent circles

Problem 11
Three identical circles of radius 30 cm are tangent to each other externally. A fourth circle of the same radius was drawn so that its center is coincidence with the center of the space bounded by the three tangent circles. Find the area of the region inside the fourth circle but outside the first three circles. It is the shaded region shown in the figure below.