$\Sigma M_A = 0$
$6R_D = 4[2(30)]$
$R_D = 40 \, \text{kN}$
$\Sigma M_D = 0$
$6R_A = 2[2(30)]$
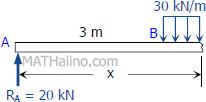
$R_A = 20 \text{kN}$
Segment AB:
$V_{AB} = 20 \, \text{kN}$
$M_{AB} = 20x \, \text{kN}\cdot\text{m}$
Segment BC:
$V_{BC} = 20 - 30(x - 3)$
$V_{BC} = 110 - 30x \, \text{kN}$
$M_{BC} = 20x - 30(x - 3)(x - 3)/2$
$M_{BC} = 20x - 15(x - 3)^2 \, \text{kN}\cdot\text{m}$
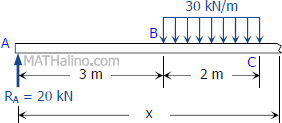Segment CD:
$V_{CD} = 20 - 30(2)$
$V_{CD} = -40 \, \text{kN}$
$M_{CD} = 20x - 30(2)(x - 4)$
$M_{CD} = 20x - 60(x - 4) \, \text{kN}\cdot\text{m}$
To draw the Shear Diagram:
- For segment AB, the shear is uniformly distributed at 20 kN.
- VBC = 110 - 30x for segment BC; at x = 3 m, VBC = 20 kN; at x = 5 m, VBC = -40 kN. For VBC = 0, x = 3.67 m or 0.67 m from B.
- The shear for segment CD is uniformly distributed at -40 kN.
To draw the Moment Diagram:
- For AB, MAB = 20x; at x = 0, MAB = 0; at x = 3 m, MAB = 60 kN·m.
- MBC = 20x - 15(x - 3)2 for segment BC is second degree curve; at x = 3 m, MBC = 60 kN·m; at x = 5 m, MBC = 40 kN·m. Note that maximum moment occurred at zero shear; at x = 3.67 m, MBC = 66.67 kN·m.
- MCD = 20x - 60(x - 4) for segment CD is linear; at x = 5 m, MCD = 40 kN·m; at x = 6 m, MCD = 0.
