Problem 403

Beam loaded as shown in Fig. P-403. See the instruction.

Solution 403

From the load diagram:
\Sigma M_B = 0
5R_D + 1(30) = 3(50)
R_D = 24 \, \text{kN}

\Sigma M_D = 0
5R_B = 2(50) + 6(30)
R_B = 56 \, \text{kN}

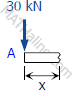Segment AB:
V_{AB} = –30 \, \text{kN}
M_{AB} = –30x \, \text{kN}\cdot\text{m}

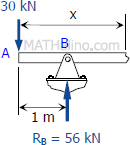Segment BC:
V_{BC} = –30 + 56
V_{BC} = 26 \, \text{kN}

M_{BC} = –30x + 56(x – 1)
M_{BC} = 26x – 56 \, \text{kN}\cdot\text{m}

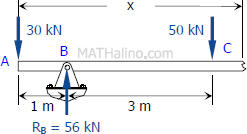Segment CD:
V_{CD} = –30 + 56 – 50
V_{CD} = –24 \, \text{kN}
M_{CD} = –30x + 56(x – 1) – 50(x – 4)
M_{CD} = –30x + 56x – 56 – 50x + 200
M_{CD} = –24x + 144 \, \text{kN}\cdot\text{m}

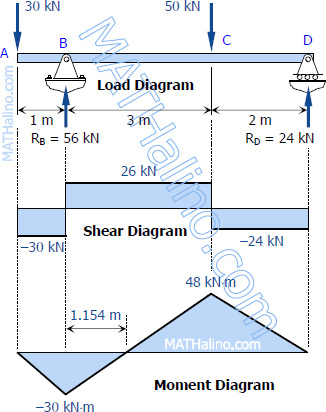To draw the Shear Diagram:

1. In segment AB, the shear is uniformly distributed over the segment at a magnitude of –30 kN.
2. In segment BC, the shear is uniformly distributed at a magnitude of 26 kN.
3. In segment CD, the shear is uniformly distributed at a magnitude of –24 kN.

To draw the Moment Diagram:

1. The equation M_AB = –30x is linear, at x = 0, M_AB = 0 and at x = 1 m, M_AB = –30 kN·m.
2. M_BC = 26x – 56 is also linear. At x = 1 m, M_BC = –30 kN·m; at x = 4 m, M_BC = 48 kN·m. When M_BC = 0, x = 2.154 m, thus the moment is zero at 1.154 m from B.
3. M_CD = –24x + 144 is again linear. At x = 4 m, M_CD = 48 kN·m; at x = 6 m, M_CD = 0.