$\Sigma M_F = 0$
$15R_A = (400 + 200)(12) + (800 + 200)(6)$
$R_A = 880 \, \text{kN}$
$\Sigma M_A = 0$
$15R_F = (400 + 200)(3) + (800 + 200)(9)$
$R_F = 720 \, \text{kN}$
At Joint A
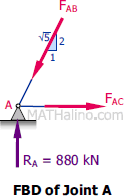$\Sigma F_V = 0$
$\frac{2}{\sqrt{5}}F_{AB} = 880$
$F_{AB} = 983.87 \, \text{kN}$ compression
$\Sigma F_H = 0$
$F_{AC} = \frac{1}{\sqrt{5}}F_{AB}$
$F_{AC} = \frac{1}{\sqrt{5}}(983.87)$
$F_{AC} = 440 \, \text{kN}$ tension
At Joint B
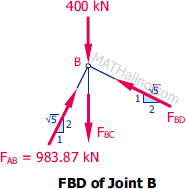$\Sigma F_H = 0$
$\frac{2}{\sqrt{5}}F_{BD} = \frac{1}{\sqrt{5}}(983.87)$
$F_{BD} = 491.94 \, \text{kN}$ compression
$\Sigma F_V = 0$
$F_{BC} + 400 = \frac{2}{\sqrt{5}}(983.87) + \frac{1}{\sqrt{5}}F_{BD}$
$F_{BC} + 400 = \frac{2}{\sqrt{5}}(983.87) + \frac{1}{\sqrt{5}}(491.94)$
$F_{BC} = 700 \, \text{kN}$ tension
At Joint C
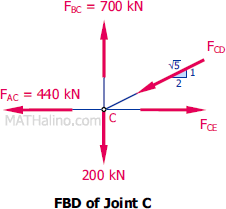$\Sigma F_V = 0$
$\frac{1}{\sqrt{5}}F_{CD} + 200 = 700$
$F_{CD} = 1118.03 \, \text{kN}$ compression
$\Sigma F_H = 0$
$F_{CE} = 440 + \frac{2}{\sqrt{5}}F_{CD}$
$F_{CE} = 440 + \frac{2}{\sqrt{5}}(1118.03)$
$F_{CE} = 1440 \, \text{kN}$ tension
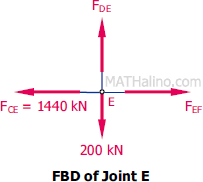At Joint E
By inspection
$F_{DE} = 200 \, \text{kN}$ tension
$F_{EF} = 1440 \, \text{kN}$ tension
At Joint D
$\Sigma F_H = 0$
$\frac{2}{\sqrt{5}}F_{DF} = \frac{2}{\sqrt{5}}(491.94) + \frac{2}{\sqrt{5}}(1118.03)$
$F_{DF} = 1609.97 \, \text{kN}$ compression
$\Sigma F_V = 0$
$\frac{1}{\sqrt{5}}F_{DE} + \frac{1}{\sqrt{5}}(1118.03) = \frac{1}{\sqrt{5}}(491.94) + 800 + 200$
$\frac{1}{\sqrt{5}}(1609.97) + \frac{1}{\sqrt{5}}(1118.03) = \frac{1}{\sqrt{5}}(491.94) + 800 + 200$
$1220 = 1220$ Check!
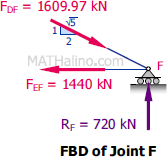At Joint F
$\Sigma F_V = 0$
$\frac{1}{\sqrt{5}}(1609.97) = 720$
$720 = 720$ Check!
$\Sigma F_H = 0$
$\frac{2}{\sqrt{5}}(1609.97) = 1440$
$1440 = 1440$ Check!
Summary
AB = 983.87 kN compression
AC = 440 kN tension
BD = 491.94 kN compression
BC = 700 kN tension
CD = 1118.03 kN compression
CE = 1440 kN tension
DE = 200 kN tension
EF = 1440 kN tension
DF = 1609.97 kN compression
With Loads at B and D moved and added to loads at C and E, respectively
RA and RF will not change, thus, internal forces of AB, AC, DF, and EF will not change.
By inspection at joint E, CE will not change because EF did not change but DE changed from 200 kN tension to 1000 kN tension.
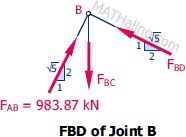By inspection at joint B, BD remains 491.94 kN compression from sum of horizontal forces but BC changed from sum of vertical forces.
$\Sigma F_V = 0$
$F_{BC} = \frac{2}{\sqrt{5}}(983.87) + \frac{1}{\sqrt{5}}F_{BD}$
$F_{BC} = \frac{2}{\sqrt{5}}(983.87) + \frac{1}{\sqrt{5}}(491.94)$
$F_{BC} = 1100 \, \text{kN}$ tension
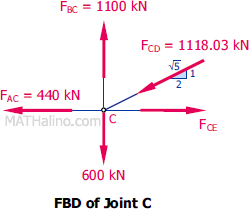At joint C
Since AC and CE did not change, the value of CD will not change in summing up forces in horizontal direction. To check,
$\Sigma F_V = 0$
$\frac{1}{\sqrt{5}}(1118.03) + 600 = 1100$
$1100 = 1100$ Check!
Thus, only BC and DE changed
- BC; from 700 kN tension to 1100 kN tension
- DE; from 200 kN tension to 1000 kN tension
