$\Sigma M_A = 0$
$12R_C = 4(900) + 18(400) + 9[(60)(18)]$
$R_C = 1710 \, \text{lb}$
$\Sigma M_C = 0$
$12R_A + 6(400) = 8(900) + 3[60(18)]$
$R_A = 670 \, \text{lb}$
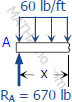 Segment AB:
Segment AB:
$V_{AB} = 670 - 60x \, \text{lb}$
$M_{AB} = 670x - 60x(x/2)$
$M_{AB} = 670x - 30x^2 \, \text{lb}\cdot\text{ft}$
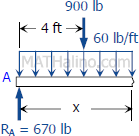 Segment BC:
Segment BC:
$V_{BC} = 670 - 900 - 60x$
$V_{BC} = -230 - 60x \, \text{lb}$
$M_{BC} = 670x - 900(x - 4) - 60x(x/2)$
$M_{BC} = 3600 - 230x - 30x^2 \, \text{lb}\cdot\text{ft}$
Segment CD:
$V_{CD} = 670 + 1710 - 900 - 60x$
$V_{CD} = 1480 - 60x \, \text{lb}$
$M_{CD} = 670x + 1710(x - 12) - 900(x - 4) - 60x(x/2)$
$M_{CD} = -16920 + 1480x - 30x^2 \, \text{lb}\cdot\text{ft}$
To draw the Shear Diagram:
- VAB = 670 - 60x for segment AB is linear; at x = 0, VAB= 670 lb; at x = 4 ft, VAB = 430 lb.
- For segment BC, VBC = -230 - 60x is also linear; at x= 4 ft, VBC = -470 lb, at x = 12 ft, VBC = -950 lb.
- VCD = 1480 - 60x for segment CD is again linear; at x = 12, VCD = 760 lb; at x = 18 ft, VCD = 400 lb.
To draw the Moment Diagram:
- MAB = 670x - 30x2 for segment AB is a second degree curve; at x = 0, MAB = 0; at x = 4 ft, MAB = 2200 lb·ft.
- For BC, MBC = 3600 - 230x - 30x2, is a second degree curve; at x = 4 ft, MBC = 2200 lb·ft, at x = 12 ft, MBC = -3480 lb·ft; When MBC = 0, 3600 - 230x - 30x2 = 0, x = -15.439 ft and 7.772 ft. Take x = 7.772 ft, thus, the moment is zero at 3.772 ft from B.
- For segment CD, MCD = -16920 + 1480x - 30x2 is a second degree curve; at x = 12 ft, MCD = -3480 lb·ft; at x = 18 ft, MCD = 0.
