Area-Moment Method | Beam Deflections

Another method of determining the slopes and deflections in beams is the area-moment method, which involves the area of the moment diagram.
 

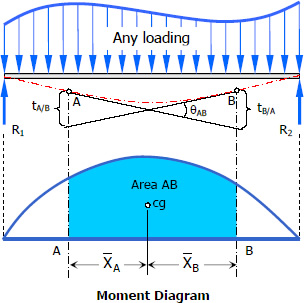
Theorems of Area-Moment Method
Theorem I
The change in slope between the tangents drawn to the elastic curve at any two points A and B is equal to the product of 1/EI multiplied by the area of the moment diagram between these two points.
 

Theorem II
The deviation of any point B relative to the tangent drawn to the elastic curve at any other point A, in a direction perpendicular to the original position of the beam, is equal to the product of 1/EI multiplied by the moment of an area about B of that part of the moment diagram between points A and B.
 

and
 

Rules of Sign

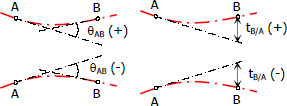
1. The deviation at any point is positive if the point lies above the tangent, negative if the point is below the tangent.
2. Measured from left tangent, if θ is counterclockwise, the change of slope is positive, negative if θ is clockwise.