Problem 1005 | Maximum concentrated load at the midspan that the reinforced timber beam can carry

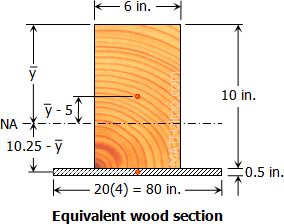
From the equivalent wood section shown
$A_w = 6(10) = 60 ~ \text{in}^2$

$A_s = 80(0.5) = 40 ~ \text{in}^2$

$A = A_w + A_s = 100 ~ \text{in}^2$
 

Location of NA from the top of the beam
$A \bar{y} = A_w y_w + A_s y_s$

$100 \bar{y} = 60(5) + 40(10.25)$

$\bar{y} = 7.1 ~ \text{in}$
 

Moment of inertia of each section
$I_g = \dfrac{bd^3}{12}$

$I_{gw} = \dfrac{6(10^3)}{12} = 500 ~ \text{in}^4$

$I_{gs} = \dfrac{80(0.5^3)}{12} = \dfrac{5}{6} ~ \text{in}^4$
 

Moment of inertia about NA
$I = \Sigma (I_g + Ad^2)$

$I_{NA} = [ \, I_{gw} + A_w(\bar{y} - 5)^2 \, ] + [ \, I_{gs} + A_s(10.25 - \bar{y})^2 \, ]$

$I_{NA} = [ \, 500 + 60(7.1 - 5)^2 \, ] + [ \, \frac{5}{6} + 40(10.25 - 7.1)^2 \, ]$

$I_{NA} = \dfrac{3487}{3} ~ \text{in}^4 = 1162.33 ~ \text{in}^4$
 

Maximum moment that the beam can carry
$f_b = \dfrac{My}{I}$

$M = \dfrac{f_bI}{y}$
 

Based on strength of wood ($y = \bar{y} = 7.1 ~ \text{in}$)
$M_w = \dfrac{1200(\frac{3487}{3})}{7.1}$

$M_w = 196\,450.70 ~ \text{lb}\cdot\text{in}$

$M_w = 16\,370.89 ~ \text{lb}\cdot\text{ft}$
 

Based on strength of wood ($y = 10.5 - \bar{y} = 3.4 ~ \text{in}$)
$M_s = \dfrac{\dfrac{18\,000}{20} \times \dfrac{3487}{3}}{3.4}$

$M_s = 307\,676.47 ~ \text{lb}\cdot\text{in}$

$M_s = 25\,639.70 ~ \text{lb}\cdot\text{ft}$

 

For safe value of M, use the smaller of the two
$M = 16\,370.89 ~ \text{lb}\cdot\text{ft}$
 

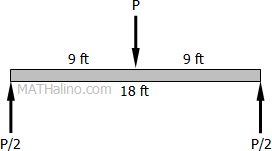Safe value of P at the midspan that beam can carry
$M = \dfrac{PL}{4}$

$16\,370.89 = \dfrac{P(18)}{4}$

$P = 3637.98 ~ \text{lb}$           answer