016 Radius of the sphere circumscribing a regular triangular pyramid

Triangles ABC and BCD are equilateral triangles. See the regular tetrahedron for more information. Triangle AGD is isosceles triangle. DE and AF are altitudes of AGD and intersect at O, thus O is the center of the circumscribing sphere. E and F are the centroids of ABC and BCD, respectively.
 

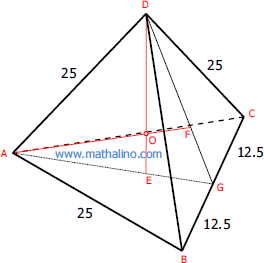From right triangle BGA
$AG^2 + BG^2 = AB^2$

$AG^2 + 12.5^2 = 25^2$

$AG = 21.65 \, \text{ cm} = DG$
 

$AE = \frac{2}{3}AG = \frac{2}{3}(21.65)$

$AE = 14.43 \, \text{ cm} = DF$
 

$EG = \frac{1}{3}AG = \frac{2}{3}(21.65)$

$EG = 7.22 \, \text{ cm} = FG$
 

From right triangle AED
$ED^2 + AE^2 = AD^2$

$ED^2 + 14.43^2 = 25^2$

$ED = 20.42 \, \text{ cm} = FA$
 

From isosceles triangle AGD
$\sin \frac{1}{2}(\angle AGD) = \dfrac{\frac{1}{2}AD}{AG}$

$\sin \frac{1}{2}(\angle AGD) = \dfrac{\frac{1}{2}(25)}{21.65}$

$\frac{1}{2}(\angle AGD) = 35.26^\circ$

$\angle AGD = 70.52^\circ$
 

From right triangle GEO
$\tan \frac{1}{2}(\angle AGD) = \dfrac{OE}{EG}$

$\tan 35.26^\circ = \dfrac{OE}{7.22}$

$OE = 5.10 \, \text{ cm} = OF$   → radius of the inscribed sphere, r
 

$OD = ED - OE = 20.42 - 5.10$

$OD = 15.32 \, \text{ cm} = OA$   → radius of the circumscribing sphere, R
 

Area of circumscribing sphere:
$A = 4\pi R^2 = 4\pi (15.32^2)$

$A = 2\,949.36 \, \text{ cm}^2$           answer
 

Volume of circumscribing sphere:
$V = \frac{4}{3}\pi R^3 = \frac{4}{3}\pi (15.32^3)$

$V = 15\,061.38 \, \text{ cm}^3$           answer

From the formula for the altitude of regular tetrahedron:

$h = \dfrac{a\sqrt{6}}{3}$

$h = \dfrac{25\sqrt{6}}{3}$

$h = 20.41 \, \text{ cm}$
 

The center of circumscribing and inscribed spheres is coincident with the centroid of regular tetrahedron. Thus,

$r = \frac{1}{4}h$   and

$R = \frac{3}{4}h$
 

$r = 5.10 \, \text{ cm}$   → radius of inscribed sphere (okay)

$R = 15.31 \, \text{ cm}$   → radius of circumscribing sphere (okay!)